0
0
Рейтинг
0.0
Оцените
Оценить
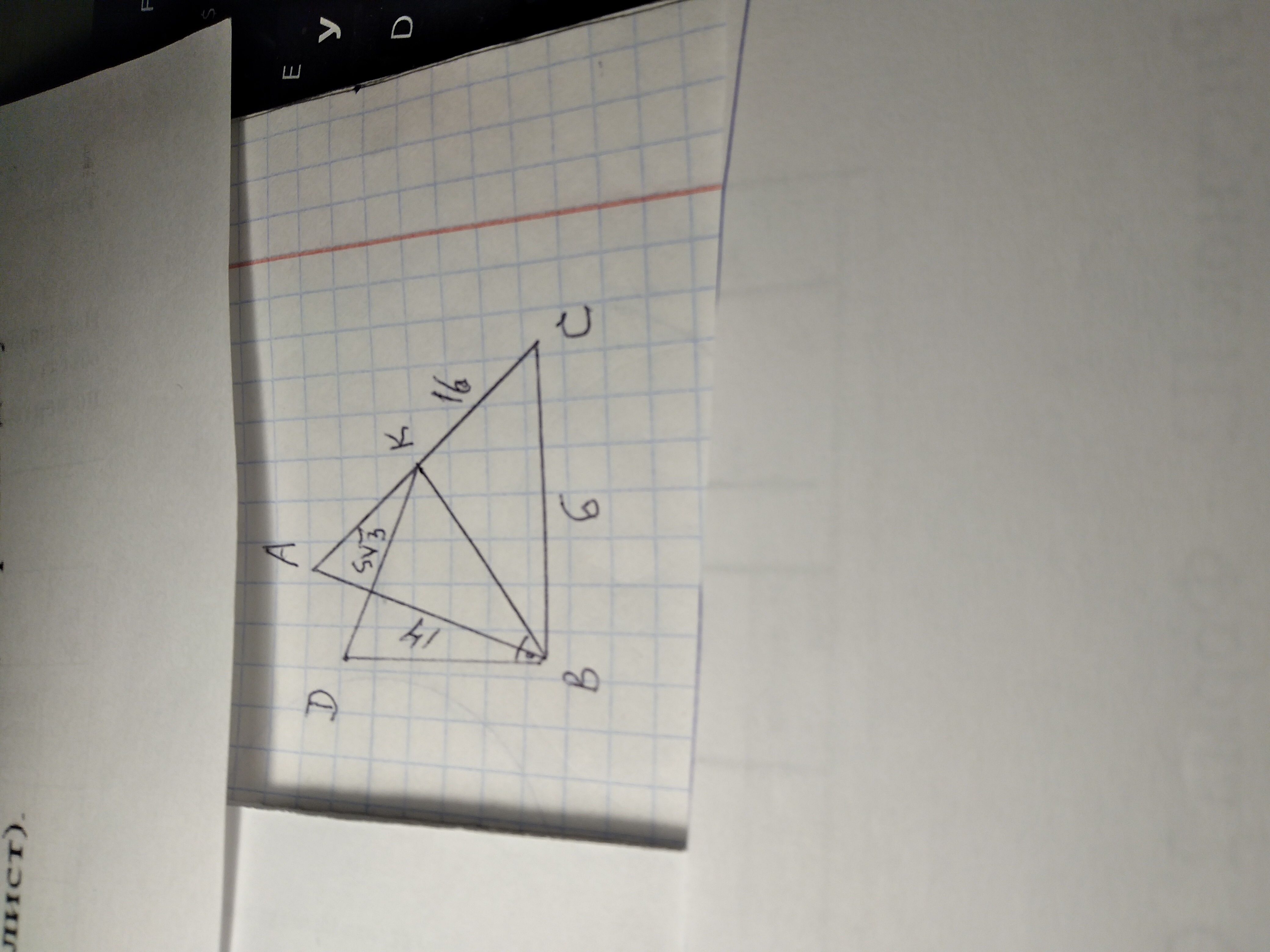
ПРОШУ НЕ БРАТИ ЧУЖУ ВІДПОВІДЬ! Сторони трикутника дорівнюють 14 см. 16 см і 6 см. Із вершини більшого кута трикутника до його площини проведено перпендикуляр. Відстань від верхнього кінця перпендикуляра до більшої сторони дорівнює 5корінь3 см. Знайдіть довжину цього перпендикуляра
Жалоба
Комментарии (0)
По дате
По дате
Популярные
Нет комментарий
Ответы
Время ожидания вывода ответов:
Последующие ответы будут показываться без ожидания.
Чтобы добавить ответ - нужно войти или зарегистрироваться