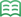
Поскольку прямые AC и EG параллельны, то угол ABD равен углу DFG как соответственные углы.

Поэтому угол DFG = угол ABD = 143 градуса.

Дано:

AC||EG

УголABC=143

УголBDF=82

Решение:

уголABH и уголEHB-внутренни односторонние углы при AC||EG и секущей BH,тогда уголABH+уголEHB=180

уголEHB-уголABH=180-143=37

•Сумма смежных углов=180

уголBDF и уголFDH-смежный,тогда BDF+FDH=180

уголFDH-уголBDF=180-82=98

Рассмотрим уголFDH

уголFDH=180-98-37=45

Ответ:уголDFG=45

градусная мера угла \( DFG \) равна 61°

Чтобы найти угол , используем свойства углов: 1. Угол  = 14. 2. Угол \( \angle bdf = 82^\circ \). Сначала найдем угол \( \angle ADB \): \[ \angle ADB = 180^\circ - 143^\circ = 37^\circ \] Теперь в треугольнике \( BDF \): \[ 82^\circ + \angle DFB + 37^\circ = 180^\circ \] Решим: \[ \angle DFB = 180^\circ - 82^\circ - 37^\circ = 61^\circ \] Таким образом, угол \( \angle dfg = 61^\circ \).